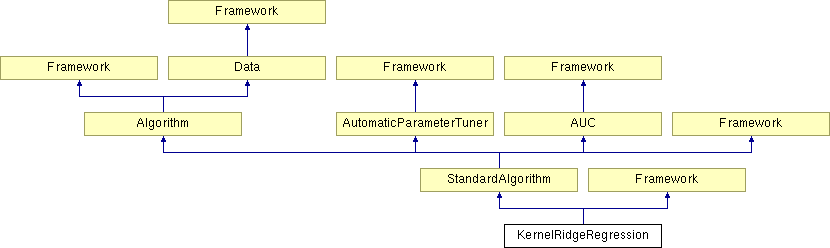
KernelRidgeRegression Class Reference

#include <KernelRidgeRegression.h>

Inheritance diagram for KernelRidgeRegression:

List of all members.

Public Member Functions
	KernelRidgeRegression ()
	~KernelRidgeRegression ()
virtual void	modelInit ()
virtual void	modelUpdate (REAL *input, REAL *target, uint nSamples, uint crossRun)
virtual void	predictAllOutputs (REAL *rawInputs, REAL *outputs, uint nSamples, uint crossRun)
virtual void	readSpecificMaps ()
virtual void	saveWeights (int cross)
virtual void	loadWeights (int cross)
virtual void	loadMetaWeights (int cross)
Static Public Member Functions
static string	templateGenerator (int id, string preEffect, int nameID, bool blendStop)
Private Attributes
REAL **	m_x
REAL *	m_trainMatrix
double	m_reg
double	m_polyScale
double	m_polyBiasPos
double	m_polyBiasNeg
double	m_polyPower
double	m_gaussSigma
double	m_tanhScale
double	m_tanhBiasPos
double	m_tanhBiasNeg
string	m_kernelType

---

Detailed Description

Kernel ridge regression Regression in a high-dimensional feature space, defined by the kernel

Tunable parameters are the regularization constant and some kernel constants

Supported kernels:

• linear
• polynomial

Definition at line 19 of file KernelRidgeRegression.h.

---

Constructor & Destructor Documentation

KernelRidgeRegression::KernelRidgeRegression

(

)

Constructor

Definition at line 8 of file KernelRidgeRegression.cpp.

{
    cout<<"KernelRidgeRegression"<<endl;
    // init member vars
    m_x = 0;
    m_reg = 0;
    m_trainMatrix = 0;
}

KernelRidgeRegression::~KernelRidgeRegression

(

)

Destructor

Definition at line 20 of file KernelRidgeRegression.cpp.

{
    cout<<"descructor KernelRidgeRegression"<<endl;
    for ( uint i=0;i<m_nCross+1;i++ )
    {
        if ( m_x )
        {
            if ( m_x[i] )
                delete[] m_x[i];
            m_x[i] = 0;
        }
    }
    if ( m_x )
        delete[] m_x;
    m_x = 0;

    if ( m_trainMatrix )
        delete[] m_trainMatrix;
    m_trainMatrix = 0;
}

---

Member Function Documentation

void KernelRidgeRegression::loadWeights

(

int

cross

)

[virtual]

Load the weights and all other parameters and make the model ready to predict

Implements StandardAlgorithm.

Definition at line 446 of file KernelRidgeRegression.cpp.

{
    char buf[1024];
    sprintf ( buf,"%02d",cross );
    string name = m_datasetPath + "/" + m_tempPath + "/" + m_weightFile + "." + buf;
    cout<<"Load:"<<name<<endl;
    fstream f ( name.c_str(), ios::in );
    if ( f.is_open() == false )
        assert ( false );
    f.read ( ( char* ) &m_nTrain, sizeof ( int ) );
    f.read ( ( char* ) &m_nFeatures, sizeof ( int ) );
    f.read ( ( char* ) &m_nClass, sizeof ( int ) );
    f.read ( ( char* ) &m_nDomain, sizeof ( int ) );

    m_x = new REAL*[m_nCross+1];
    for ( int i=0;i<m_nCross+1;i++ )
        m_x[i] = 0;
    m_x[cross] = new REAL[m_nTrain * m_nClass * m_nDomain];

    m_trainMatrix = new REAL[m_nTrain*m_nFeatures];

    f.read ( ( char* ) m_x[cross], sizeof ( REAL ) *m_nTrain*m_nClass*m_nDomain );
    f.read ( ( char* ) m_trainMatrix, sizeof ( REAL ) *m_nTrain*m_nFeatures );
    f.read ( ( char* ) &m_maxSwing, sizeof ( double ) );
    f.read ( ( char* ) &m_reg, sizeof ( double ) );
    f.read ( ( char* ) &m_polyScale, sizeof ( double ) );
    f.read ( ( char* ) &m_polyBiasPos, sizeof ( double ) );
    f.read ( ( char* ) &m_polyBiasNeg, sizeof ( double ) );
    f.read ( ( char* ) &m_polyPower, sizeof ( double ) );
    f.read ( ( char* ) &m_gaussSigma, sizeof ( double ) );
    f.read ( ( char* ) &m_tanhScale, sizeof ( double ) );
    f.read ( ( char* ) &m_tanhBiasPos, sizeof ( double ) );
    f.read ( ( char* ) &m_tanhBiasNeg, sizeof ( double ) );
    f.close();
}

void KernelRidgeRegression::modelInit

(

)

[virtual]

Init the Linear Model

Implements StandardAlgorithm.

Definition at line 66 of file KernelRidgeRegression.cpp.

{
    // add the tunable parameter
    paramDoubleValues.push_back ( &m_reg );
    paramDoubleNames.push_back ( "reg" );

    if ( m_kernelType == "Poly" )
    {
        paramDoubleValues.push_back ( &m_polyScale );
        paramDoubleNames.push_back ( "polyScale" );
        if ( m_polyBiasPos != 0.0 )
        {
            paramDoubleValues.push_back ( &m_polyBiasPos );
            paramDoubleNames.push_back ( "polyBiasPos" );
        }
        if ( m_polyBiasNeg != 0.0 )
        {
            paramDoubleValues.push_back ( &m_polyBiasNeg );
            paramDoubleNames.push_back ( "polyBiasNeg" );
        }
        paramDoubleValues.push_back ( &m_polyPower );
        paramDoubleNames.push_back ( "polyPower" );
    }

    if ( m_kernelType == "Gauss" )
    {
        paramDoubleValues.push_back ( &m_gaussSigma );
        paramDoubleNames.push_back ( "gaussSigma" );
    }

    if ( m_kernelType == "Tanh" )
    {
        paramDoubleValues.push_back ( &m_tanhScale );
        paramDoubleNames.push_back ( "tanhScale" );
        if ( m_tanhBiasPos != 0.0 )
        {
            paramDoubleValues.push_back ( &m_tanhBiasPos );
            paramDoubleNames.push_back ( "tanhBiasPos" );
        }
        if ( m_tanhBiasNeg != 0.0 )
        {
            paramDoubleValues.push_back ( &m_tanhBiasNeg );
            paramDoubleNames.push_back ( "tanhBiasNeg" );
        }
    }

    // alloc mem for weights
    if ( m_x == 0 )
    {
        m_x = new REAL*[m_nCross+1];
        for ( uint i=0;i<m_nCross+1;i++ )
            m_x[i] = new REAL[m_nTrain * m_nClass * m_nDomain];
    }
}

void KernelRidgeRegression::modelUpdate	(	REAL *	input,
		REAL *	target,
		uint	nSamples,
		uint	crossRun
	)			[virtual]

Make a model update, set the new cross validation set or set the whole training set for retraining

Parameters:

	input	Pointer to input (can be cross validation set, or whole training set) (rows x nFeatures)
	target	The targets (can be cross validation targets)
	nSamples	The sample size (rows) in input
	crossRun	The cross validation run (for training)

Implements StandardAlgorithm.

Definition at line 269 of file KernelRidgeRegression.cpp.

{
    // gram matrix
    REAL* K = new REAL[nSamples*nSamples];
    REAL* y = new REAL[nSamples*m_nClass*m_nDomain];

    int lda = nSamples, nrhs = m_nClass*m_nDomain, ldb = nSamples, info = -1, maxStabilizeEpochs = 3, stabilizeEpoch = 0;

    // do Cholesky factorization until it becomes stable
    while ( info != 0 && stabilizeEpoch < maxStabilizeEpochs )
    {
        if ( m_kernelType == "Linear" )
        {
            CBLAS_GEMM ( CblasRowMajor, CblasNoTrans, CblasTrans, nSamples, nSamples, m_nFeatures, 1.0, input, m_nFeatures, input, m_nFeatures, 0.0, K, nSamples );
        }
        else if ( m_kernelType == "Poly" )
        {
            CBLAS_GEMM ( CblasRowMajor, CblasNoTrans, CblasTrans, nSamples, nSamples, m_nFeatures, 1.0, input, m_nFeatures, input, m_nFeatures, 0.0, K, nSamples );

            V_MULCI ( m_polyScale, K, nSamples*nSamples );
            V_ADDCI ( m_polyBiasPos - m_polyBiasNeg, K, nSamples*nSamples );

            // slower, but memory efficient
            for ( uint i=0;i<nSamples*nSamples;i++ )
            {
                if ( K[i]>=0.0 )
                    K[i] = pow ( K[i], m_polyPower );
                else
                    K[i] = -pow ( -K[i], m_polyPower );
            }
        }
        else if ( m_kernelType == "Gauss" )
        {
            // this code is slower, but correct
            /*for(uint i=0;i<nSamples;i++)
            {
                REAL *ptr0 = input + i*m_nFeatures;
                for(uint j=0;j<nSamples;j++)
                {
                    REAL *ptr1 = input + j*m_nFeatures;

                    double sum = 0.0;
                    for(uint k=0;k<m_nFeatures;k++)
                        sum += (ptr0[k] - ptr1[k]) * (ptr0[k] - ptr1[k]);

                    K[i*nSamples+j] = exp(-sum/(m_gaussSigma*m_gaussSigma));
                }
            }*/
            // speedup calculation by using BLAS in x'y: ||x-y||^2 = sum(x.^2) - 2 * x'y + sum(y.^2)
            REAL* squaredSum = new REAL[nSamples];
            for ( uint i=0;i<nSamples;i++ )
            {
                double sum = 0.0;
                REAL *ptr = input + i*m_nFeatures;
                for ( uint k=0;k<m_nFeatures;k++ )
                    sum += ptr[k]*ptr[k];
                squaredSum[i] = sum;
            }

            CBLAS_GEMM ( CblasRowMajor, CblasNoTrans, CblasTrans, nSamples, nSamples, m_nFeatures, 1.0, input, m_nFeatures, input, m_nFeatures, 0.0, K, nSamples );

            for ( uint i=0;i<nSamples;i++ )
            {
                REAL *ptr = K + i*nSamples, sqSum = squaredSum[i];
                for ( uint j=0;j<nSamples;j++ )
                    ptr[j] = sqSum + squaredSum[j] - 2.0 * ptr[j];  // sum = sum_k (ptr0[k] - ptr1[k]) * (ptr0[k] - ptr1[k])
            }

            REAL c0 = - 1.0 / ( m_gaussSigma * m_gaussSigma );
            for ( uint i=0;i<nSamples*nSamples;i++ )
                K[i] *= c0;

            // block-wise apply of the exp-function
            uint blockSize = 10000000;
            assert ( nSamples*nSamples < 4200000000 );
            for ( uint i=0;i<nSamples*nSamples && i<4200000000;i+=blockSize )
            {
                int nElem = nSamples*nSamples - i;
                if ( nSamples*nSamples - i > blockSize )
                    nElem = blockSize;
                V_EXP ( K+i, nElem );
            }

            delete[] squaredSum;
        }
        else if ( m_kernelType == "Tanh" )
        {
            CBLAS_GEMM ( CblasRowMajor, CblasNoTrans, CblasTrans, nSamples, nSamples, m_nFeatures, 1.0, input, m_nFeatures, input, m_nFeatures, 0.0, K, nSamples );

            V_MULCI ( m_tanhScale, K, nSamples*nSamples );
            V_ADDCI ( m_tanhBiasPos - m_tanhBiasNeg, K, nSamples*nSamples );
            V_TANH ( nSamples*nSamples, K, K );
        }
        else
            assert ( false );

        for ( uint i=0;i<nSamples;i++ )
            K[i+i*nSamples] += ( REAL ) nSamples * m_reg;

        // copy targets to a tmp matrix
        for ( uint i=0;i<nrhs;i++ )
            for ( uint j=0;j<nSamples;j++ )
                y[j+i*nSamples] = target[i+j*nrhs];  // copy to colMajor

        //Cholesky factorization of a symmetric (Hermitian) positive-definite matrix
        LAPACK_POTRF ( "U", &lda, K, &lda, &info );

        // no stabilizing in cross-fold training
        if ( crossRun != m_nCross )
            info = 0;

        if ( info != 0 )
        {
            m_reg *= 1.1;
            cout<<"[retraining] Stabilize reg:"<<m_reg<<"  (info:"<<info<<")"<<endl;
            stabilizeEpoch++;
        }
    }

    // Solves a system of linear equations with a Cholesky-factored symmetric (Hermitian) positive-definite matrix
    LAPACK_POTRS ( "U", &lda, &nrhs, K, &lda, y, &ldb, &info );  // Y=solution vector

    if ( info != 0 )
        cout<<"error: equation solver failed to converge: "<<info<<endl;

    for ( uint i=0;i<nSamples;i++ )
        for ( uint j=0;j<m_nClass*m_nDomain;j++ )
            m_x[crossRun][j+i*m_nClass*m_nDomain] = y[i+j*nSamples];  // copy to rowMajor

    delete[] y;
    delete[] K;
}

void KernelRidgeRegression::predictAllOutputs	(	REAL *	rawInputs,
		REAL *	outputs,
		uint	nSamples,
		uint	crossRun
	)			[virtual]

Prediction for outside use, predicts outputs based on raw input values

Parameters:

	rawInputs	The input feature, without normalization (raw)
	outputs	The output value (prediction of target)
	nSamples	The input size (number of rows)
	crossRun	Number of cross validation run (in training)

Implements StandardAlgorithm.

Definition at line 129 of file KernelRidgeRegression.cpp.

{
    REAL *K, *A;
    uint m, n = m_nFeatures;

    // predict mode
    if ( Framework::getFrameworkMode() == 1 )
    {
        A = m_trainMatrix;
        K = new REAL[nSamples*m_nTrain];
        m = m_nTrain;
    }
    else  // train mode
    {
        A = m_validationType=="ValidationSet" ? m_trainOrig : m_train[crossRun];
        K = new REAL[nSamples*m_trainSize[crossRun]];
        m = m_trainSize[crossRun];
    }

    if ( m_kernelType == "Linear" )
    {
        CBLAS_GEMM ( CblasRowMajor, CblasNoTrans, CblasTrans, nSamples, m, n, 1.0, rawInputs, n, A, n, 0.0, K, m );  // K = rawInputs*A'
    }
    else if ( m_kernelType == "Poly" )
    {
        CBLAS_GEMM ( CblasRowMajor, CblasNoTrans, CblasTrans, nSamples, m, n, 1.0, rawInputs, n, A, n, 0.0, K, m );  // K = rawInputs*A'

        V_MULCI ( m_polyScale, K, m*nSamples );
        V_ADDCI ( m_polyBiasPos - m_polyBiasNeg, K, m*nSamples );

        for ( uint i=0;i<m*nSamples;i++ )
        {
            if ( K[i]>=0.0 )
                K[i] = pow ( K[i], m_polyPower );
            else
                K[i] = -pow ( -K[i], m_polyPower );
        }
    }
    else if ( m_kernelType == "Gauss" )
    {
        // this code is slower, but correct
        /*for(uint i=0;i<nSamples;i++)
        {
            REAL *ptr0 = rawInputs + i*m_nFeatures;
            for(uint j=0;j<m;j++)
            {
                REAL *ptr1 = A + j*m_nFeatures;

                double sum = 0.0;
                for(uint k=0;k<m_nFeatures;k++)
                    sum += (ptr0[k] - ptr1[k]) * (ptr0[k] - ptr1[k]);

                K[i*m+j] = exp(-sum/(m_gaussSigma*m_gaussSigma));
            }
        }*/
        // speedup calculation by using BLAS in x'y: ||x-y||^2 = sum(x.^2) - 2 * x'y + sum(y.^2)
        REAL* squaredSumInputs = new REAL[nSamples];
        REAL* squaredSumData = new REAL[m];
        for ( uint i=0;i<nSamples;i++ )
        {
            double sum = 0.0;
            REAL *ptr = rawInputs + i*m_nFeatures;
            for ( uint k=0;k<m_nFeatures;k++ )
                sum += ptr[k]*ptr[k];
            squaredSumInputs[i] = sum;  // input feature squared sum
        }
        for ( uint i=0;i<m;i++ )
        {
            double sum = 0.0;
            REAL *ptr = A + i*m_nFeatures;
            for ( uint k=0;k<m_nFeatures;k++ )
                sum += ptr[k]*ptr[k];
            squaredSumData[i] = sum;  // data feature squared sun
        }

        CBLAS_GEMM ( CblasRowMajor, CblasNoTrans, CblasTrans, nSamples, m, n, 1.0, rawInputs, n, A, n, 0.0, K, m );  // K = rawInputs*A'

        for ( uint i=0;i<nSamples;i++ )
        {
            REAL* ptr = K + i*m, sqSumIn = squaredSumInputs[i];
            for ( uint j=0;j<m;j++ )
                ptr[j] = squaredSumData[j] + sqSumIn - 2.0 * ptr[j];
        }

        REAL c0 = - 1.0 / ( m_gaussSigma * m_gaussSigma );
        for ( uint i=0;i<m*nSamples;i++ )
            K[i] *= c0;

        // block-wise apply of the exp-function (due to limits in the V_EXP)
        uint blockSize = 10000000;
        assert ( m*nSamples < 4200000000 );
        for ( uint i=0;i<m*nSamples && i<4200000000;i+=blockSize )
        {
            int nElem = m*nSamples - i;
            if ( m*nSamples - i > blockSize )
                nElem = blockSize;
            V_EXP ( K+i, nElem );
        }

        delete[] squaredSumInputs;
        delete[] squaredSumData;
    }
    else if ( m_kernelType == "Tanh" )
    {
        CBLAS_GEMM ( CblasRowMajor, CblasNoTrans, CblasTrans, nSamples, m, n, 1.0, rawInputs, n, A, n, 0.0, K, m );  // K = rawInputs*A'
        V_MULCI ( m_tanhScale, K, m*nSamples );
        V_ADDCI ( m_tanhBiasPos - m_tanhBiasNeg, K, m*nSamples );
        //for(int i=0;i<m*nSamples;i++)
        //    cout<<K[i]<<" "<<flush;
        V_TANH ( m*nSamples, K, K );
    }
    else
        assert ( false );

    for ( uint i=0;i<nSamples;i++ )
    {
        for ( uint j=0;j<m_nClass*m_nDomain;j++ )
        {
            double sum = 0.0;
            REAL* ptr = K + i*m;
            for ( uint k=0;k<m;k++ )
                sum += ptr[k] * m_x[crossRun][k*m_nClass*m_nDomain + j];
            if ( isnan ( sum ) || isinf ( sum ) )
                sum = 0.0;
            outputs[i*m_nClass*m_nDomain + j] = sum;
        }
    }

    delete[] K;
}

void KernelRidgeRegression::readSpecificMaps

(

)

[virtual]

Read the Algorithm specific values from the description file

Implements StandardAlgorithm.

Definition at line 45 of file KernelRidgeRegression.cpp.

{
    m_reg = m_doubleMap["initReg"];
    m_kernelType = m_stringMap["kernelType"];

    m_polyScale = m_doubleMap["polyScaleInit"];
    m_polyBiasPos = m_doubleMap["polyBiasPosInit"];
    m_polyBiasNeg = m_doubleMap["polyBiasNegInit"];
    m_polyPower = m_doubleMap["polyPowerInit"];

    m_gaussSigma = m_doubleMap["gaussSigmaInit"];

    m_tanhScale = m_doubleMap["tanhScaleInit"];
    m_tanhBiasPos = m_doubleMap["tanhBiasPosInit"];
    m_tanhBiasNeg = m_doubleMap["tanhBiasNegInit"];
}

void KernelRidgeRegression::saveWeights

(

int

cross

)

[virtual]

Save the weights and all other parameters for load the complete prediction model

Implements StandardAlgorithm.

Definition at line 406 of file KernelRidgeRegression.cpp.

{
    char buf[1024];
    sprintf ( buf,"%02d",cross );
    string name = m_datasetPath + "/" + m_tempPath + "/" + m_weightFile + "." + buf;
    if ( m_inRetraining )
        cout<<"Save:"<<name<<endl;
    fstream f ( name.c_str(), ios::out );
    f.write ( ( char* ) &m_nTrain, sizeof ( int ) );
    f.write ( ( char* ) &m_nFeatures, sizeof ( int ) );
    f.write ( ( char* ) &m_nClass, sizeof ( int ) );
    f.write ( ( char* ) &m_nDomain, sizeof ( int ) );
    f.write ( ( char* ) m_x[cross], sizeof ( REAL ) *m_nTrain*m_nClass*m_nDomain );
    if(m_validationType == "ValidationSet")
        f.write ( ( char* ) m_trainOrig, sizeof ( REAL ) *m_nTrain*m_nFeatures );
    else
    {
        if(m_enableSaveMemory && m_train[cross]==0)
            fillNCrossValidationSet (cross);
        f.write ( ( char* ) m_train[cross], sizeof ( REAL ) *m_nTrain*m_nFeatures );
        if ( m_enableSaveMemory && m_train[cross]==0)
            freeNCrossValidationSet (cross);
    }
    f.write ( ( char* ) &m_maxSwing, sizeof ( double ) );
    f.write ( ( char* ) &m_reg, sizeof ( double ) );
    f.write ( ( char* ) &m_polyScale, sizeof ( double ) );
    f.write ( ( char* ) &m_polyBiasPos, sizeof ( double ) );
    f.write ( ( char* ) &m_polyBiasNeg, sizeof ( double ) );
    f.write ( ( char* ) &m_polyPower, sizeof ( double ) );
    f.write ( ( char* ) &m_gaussSigma, sizeof ( double ) );
    f.write ( ( char* ) &m_tanhScale, sizeof ( double ) );
    f.write ( ( char* ) &m_tanhBiasPos, sizeof ( double ) );
    f.write ( ( char* ) &m_tanhBiasNeg, sizeof ( double ) );
    f.close();
}

string KernelRidgeRegression::templateGenerator	(	int	id,
		string	preEffect,
		int	nameID,
		bool	blendStop
	)			[static]

Generates a template of the description file

Returns:

The template string

Definition at line 522 of file KernelRidgeRegression.cpp.

{
    stringstream s;
    s<<"ALGORITHM=KernelRidgeRegression"<<endl;
    s<<"ID="<<id<<endl;
    s<<"TRAIN_ON_FULLPREDICTOR="<<preEffect<<endl;
    s<<"DISABLE=0"<<endl;
    s<<endl;
    s<<"[int]"<<endl;
    s<<"maxTuninigEpochs=20"<<endl;
    s<<endl;
    s<<"[double]"<<endl;
    s<<"initMaxSwing=1.0"<<endl;
    s<<"initReg=0.1"<<endl;
    s<<"polyScaleInit=1.0"<<endl;
    s<<"polyBiasPosInit=10.0"<<endl;
    s<<"polyBiasNegInit=0.01"<<endl;
    s<<"polyPowerInit=6.0"<<endl;
    s<<"gaussSigmaInit=5.0"<<endl;
    s<<"tanhScaleInit=1.0"<<endl;
    s<<"tanhBiasPosInit=0.1"<<endl;
    s<<"tanhBiasNegInit=0.1"<<endl;
    s<<"[bool]"<<endl;
    s<<"enableClipping=1"<<endl;
    s<<"enableTuneSwing=0"<<endl;
    s<<endl;
    s<<"minimzeProbe="<< ( !blendStop ) <<endl;
    s<<"minimzeProbeClassificationError=0"<<endl;
    s<<"minimzeBlend="<<blendStop<<endl;
    s<<"minimzeBlendClassificationError=0"<<endl;
    s<<endl;
    s<<"[string]"<<endl;
    s<<"kernelType=Gauss"<<endl;
    s<<"weightFile="<<"KernelRidgeRegression_"<<nameID<<"_weights.dat"<<endl;
    s<<"fullPrediction=KernelRidgeRegression_"<<nameID<<".dat"<<endl;

    return s.str();
}

---

The documentation for this class was generated from the following files:

• ELF/KernelRidgeRegression.h
• ELF/KernelRidgeRegression.cpp